先放链接:

[图形技术科普] 如何以通俗易懂的方式理解柏林噪声的原理？经典柏林噪声算法的探讨与实现 | Acerola’s Applied Graphics_哔哩哔哩_bilibili

前者能够稍微了解噪声原理, 后者则是原理讲解与实现.

本文基于Unity实现噪声可视化. 项目链接: 噪声可视化

项目演示: Unity伪噪声可视化演示[柏林噪声&单形噪声&哈希函数&值噪声]_哔哩哔哩_bilibili

项目代码涉及很多为了手动向量化而做的计算. 可能与文章代码有部分冲突, 但计算逻辑是相同的. 在这篇文章中, 代码更多的是用于帮助理解以及为实现提供参考, 细节上不必太过纠结. 如果在代码上有比较困惑的地方可以在评论区说下, 我会在文章中补充说明. 感谢您!

如果在看完本文后希望亲自实现项目中的效果, 强烈推荐跟一遍catlike coding的原文.

生成伪随机数 -- 哈希函数 Hash

伪随机数是噪声生成的基础. 而在本文中, 对于一个用于伪随机数生成的函数, 我们希望其能有一些特点:

其一, 用一个seed可以生成一个随机数. 并且, 我们假设这个seed是个uint类型的值, 那么应该满足, 连续的seed(比如0, 1, 2)对应的伪随机数之间差异足够大.

其二, 生成的伪随机数可以"吃掉"另外一个uint类型的值, 从而生成另外一个伪随机数.

其三, 我们希望伪随机数可以转为一个范围在0到1之间的浮点数, 这有利于后续使用.

其四, 对于任意一个伪随机数, 都是可重复生成的. 亦即: 相同的输入必有相同的输出.

在catlike coding中, 作者基于XXHash项目, 将其修改成了SmallXXHash, 其具体的实现原理在此就不一一讲解, 这里会给出代码实现以及大概描述.

在结构体地开头, 给出了五个质数, 这是XXHash项目作者凭经验选择的五个数. 这五个质数将用于后续的各个操作.

public readonly struct SmallXXHash {

	const uint primeA = 0b10011110001101110111100110110001;
	const uint primeB = 0b10000101111010111100101001110111;
	const uint primeC = 0b11000010101100101010111000111101;
	const uint primeD = 0b00100111110101001110101100101111;
	const uint primeE = 0b00010110010101100110011110110001;

本函数中, 伪随机数的实现主要是基于上面这五个数, 以及一个累加器.

readonly uint accumulator;

我们定义一个用uint类型的值初始化SmallXXHash的方法:

public SmallXXHash(uint accumulator){
    this.accumulator = accumulator;
}

同理定义一个隐式类型转换, 从uint到SmallXXHash:

public static implicit operator SmallXXHash(uint accumulator) => 
    new SmallXXHash(accumulator);

差不多这几步实现了从uint到SmallXXHash的转换.

而更重要的是从SmallXXHash到uint的转换:

  public static implicit operator uint(SmallXXHash hash) {
      uint avalanche = hash.accumulator;
      avalanche ^= avalanche >> 15;
      avalanche *= primeB;
avalanche ^= avalanche >> 13;
avalanche *= primeC;
avalanche ^= avalanche >> 16;
return avalanche;
  }

这样就实现了基于累加器生成一个随机数.

上面这几步属于实现了生成伪随机数的基础功能. 下面我们来实现"吃"

static uint RotateLeft(uint data, int steps) => 
    (data << steps) | (data >> 32 - steps );

public SmallXXHash Eat(int data) => 
    RotateLeft((uint)data * primeC + accumulator, 17) * primeD;

"吃"掉一个数的操作是基于二进制向左旋转的. 而用于旋转的数就基于吃掉的数和累加器中的值.

我们在很多地方乘上了开头那五个质数, 这保证了足够随机.

用种子生成随机数比较简单:

public static SmallXXHash Seed(int seed) => (uint)seed + primeE;

这里直接返回了uint类型是因为我们前面定义好了隐式类型转换函数.

最后一步就是完成从SmallXXHash到浮点数的转换.这里给出部分参考:

public uint BytesA => (uint)this & 255;
public float Floats01A => (float)BytesA * (1f / 255f);

简单来说, 先将随机数与255做位与运算, 就能将其转化为0到255之间的一个数, 然后除以255即可.

这种方式可以拓展至更多位:

  public uint GetBits (int count, int shift) =>
((uint)this >> shift) & (uint)((1 << count) - 1);

  public float GetBitsAsFloats01 (int count, int shift) =>
(float)GetBits(count, shift) * (1f / ((1 << count) - 1));

简单来说就是将255替换为可配置的一个数, 同时也让随机数能够移动可配置的位数.

至此, 三个特点我们都完成了, 而对于第四点, 也显然成立, 因为都是相同的运算.

域尺度(domain scale)

定义域尺度的目的是希望能够像变换三维坐标(缩放, 移动, 旋转)那样变换我们的噪声. 还记得我们伪随机数生成的时候, 有"吃"这个操作吗? 我们把一个三维坐标的三个分量喂给SmallXXHash, 就生成了一个伪随机数. 而这个伪随机数将会随着三维坐标的变化而变化.

实际上原理讲到这里已经非常清晰了, 实现上也没有什么麻烦的地方. 我们定义一个Domian类型, 让其拥有三个float3属性: transform, rotation和scale. 然后将其序列化, 显示在脚本组件面板中, 使其可配置即可.

之后, 根据这三个属性生成变换矩阵, 最后在生成hash的时候将变换后的三个分量分别喂给SmallXXHash即可.

另外, 由于其三个分量有可能是浮点型, 所以我们最好将坐标分量向下取整后转为整数.

值噪声 Value Noise

两个相邻的整数将生成两个随机数, 此时若取这两个整数之间的小数, 让其对应的随机数等于那两个随机数插值后得到的数, 即为值噪声.

对于一维的情况, 如上所述, 其插值方式即为线性插值.

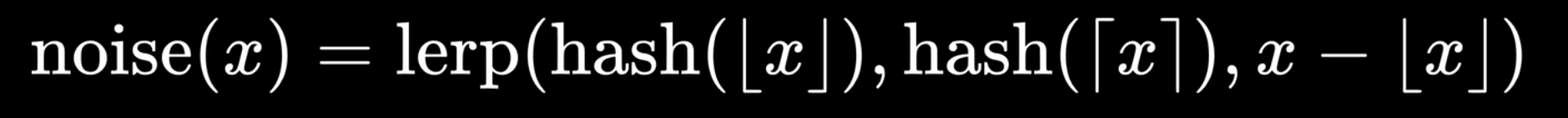
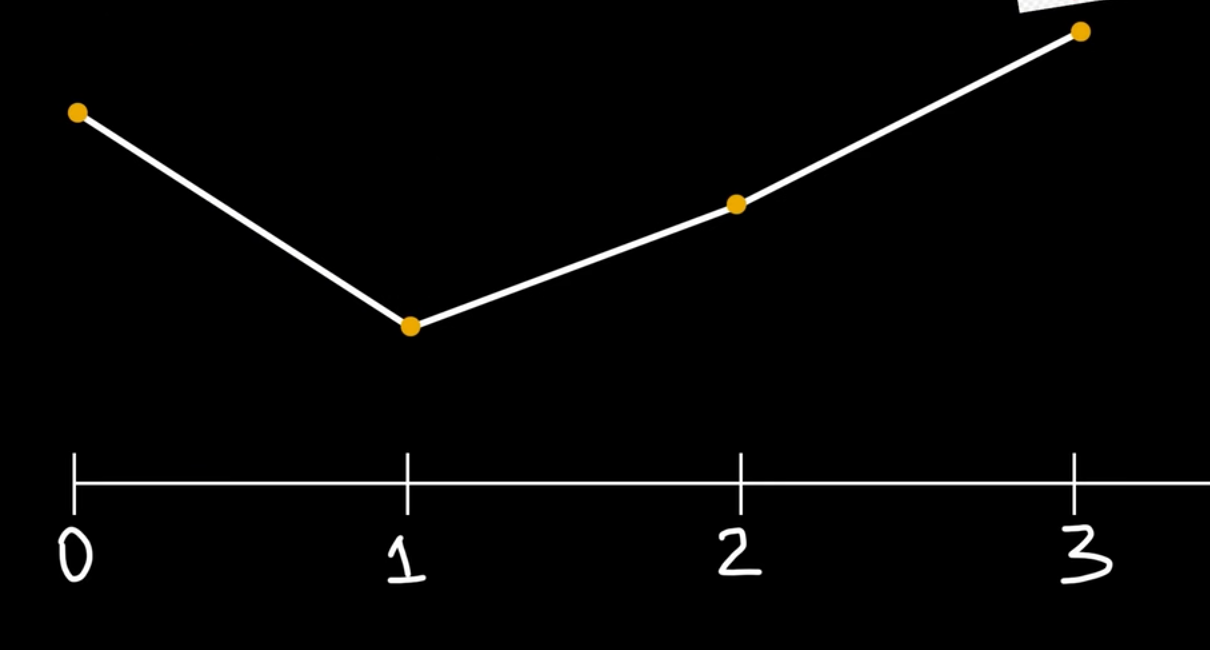
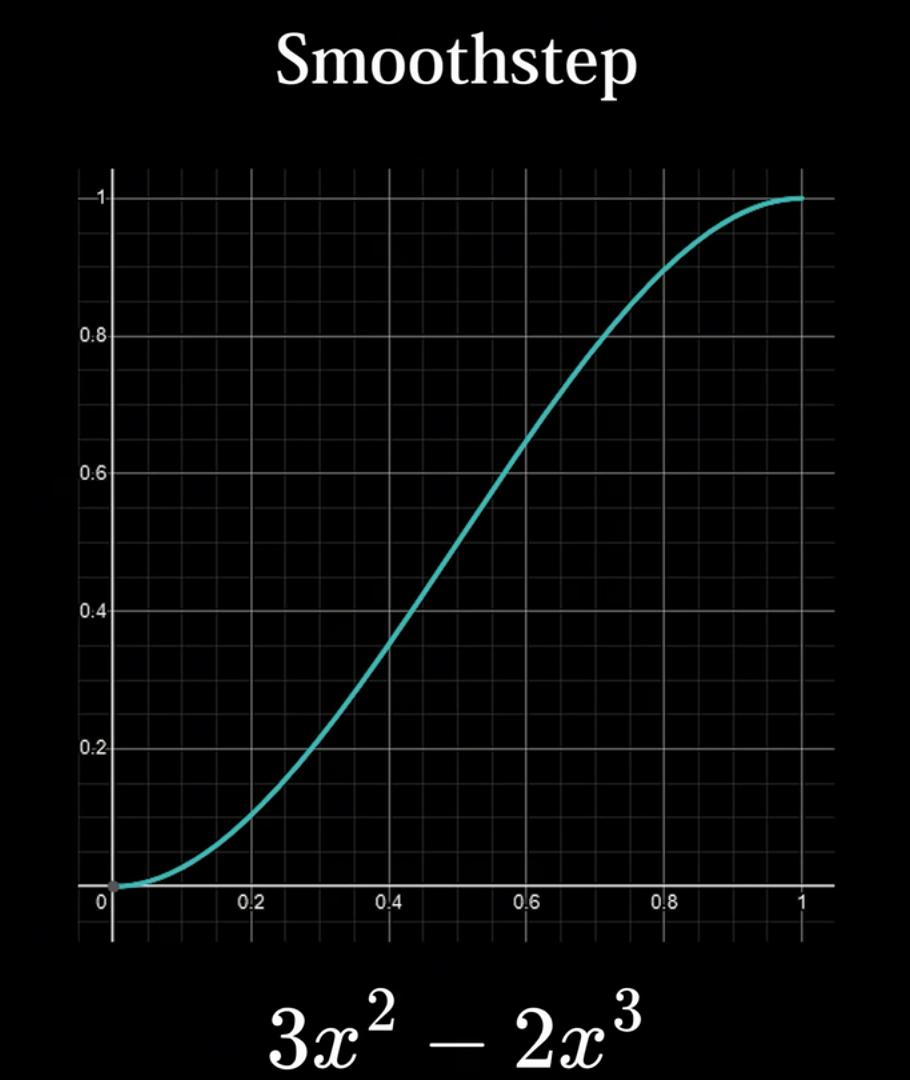
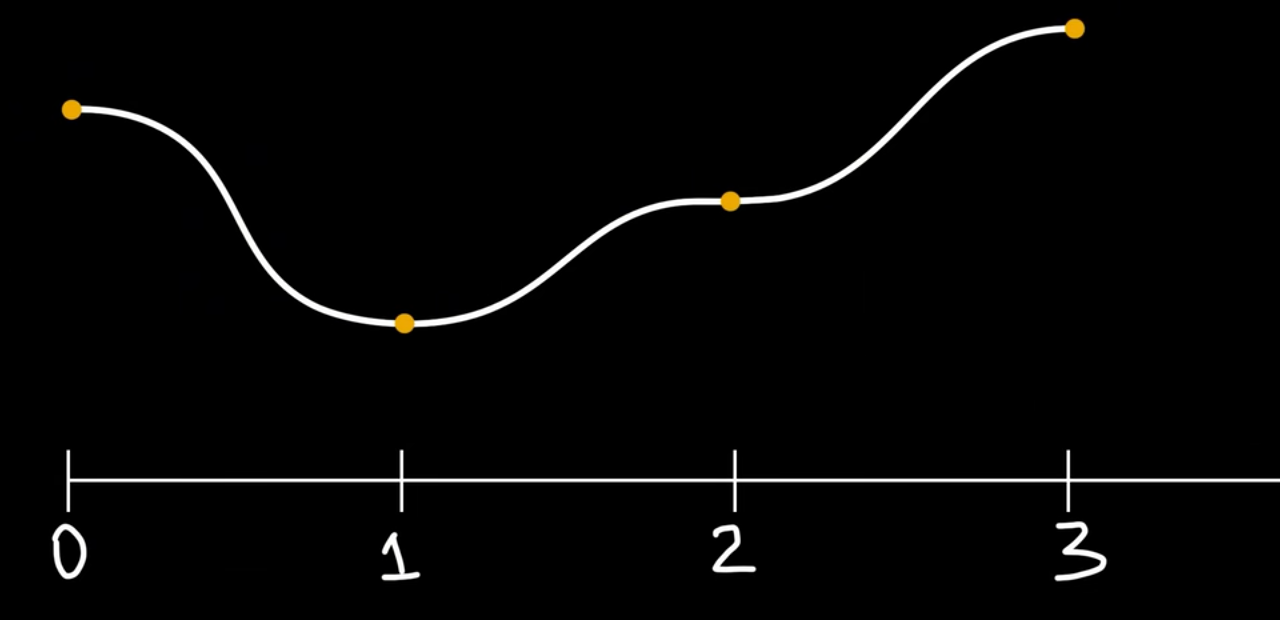
可以看到, 使用线性插值得到的值噪声依旧比较生硬. 实际上, lerp函数的最后一个参数决定了混合效果. 我们可以使用缓动函数(easing function)来作为lerp函数的最后一个参数, 其中最常用的缓动函数是smoothstep(平滑步进)函数.

对于二维的情况, 则"两个相邻整数"将变为"同一个网格中的四个顶点". 此时对于给定的输入位置, 我们再次对x, y分量向上, 向下取整, 获得邻近的顶点坐标, 然后x方向上插值两次, y方向上插值一次, 得到结果.

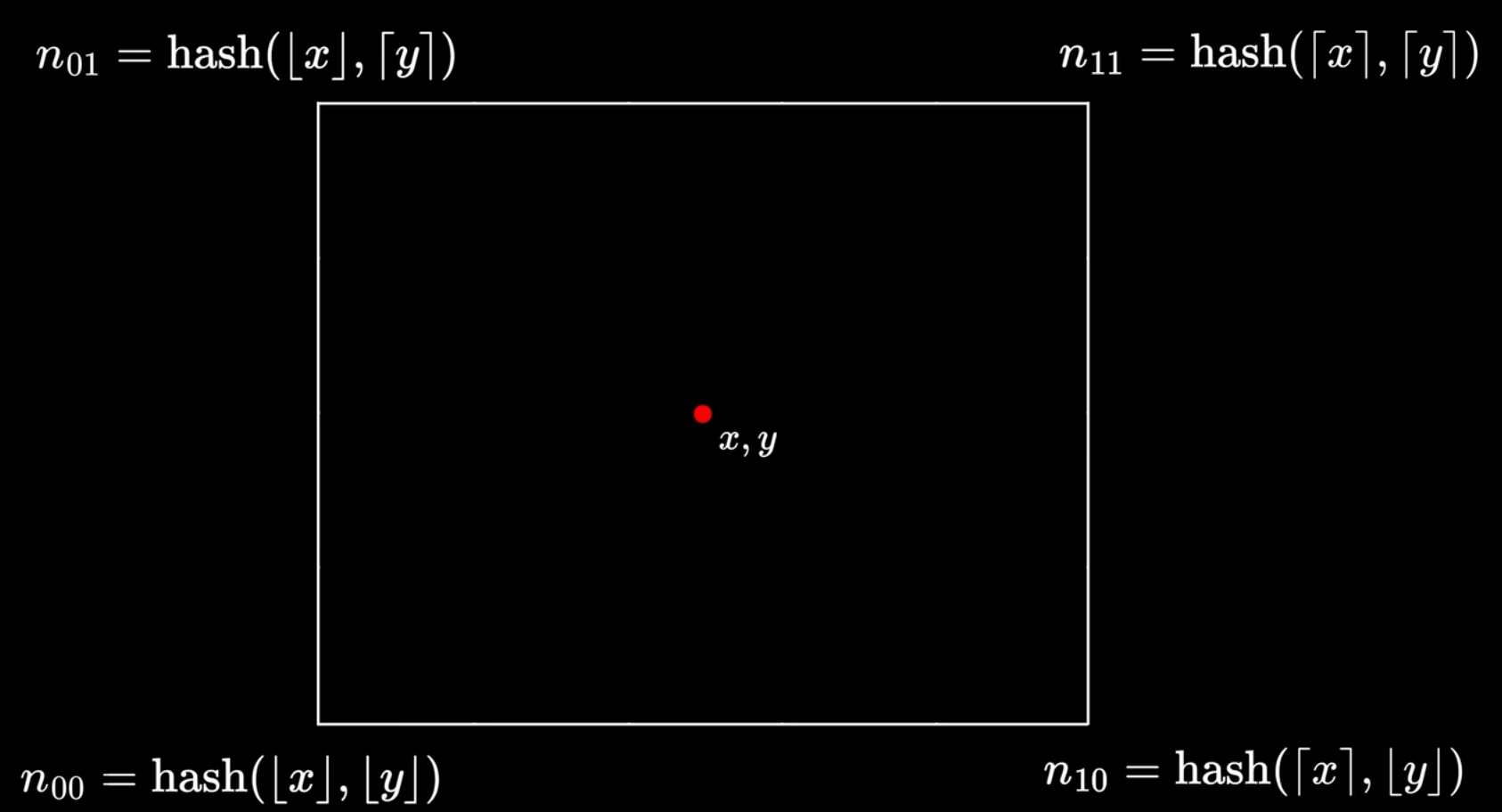
对于三维, 甚至更高维的情况同理.

关于二维的情况, 这里可以再展开一些细节(或者说强调一些内容):

首先, 四个角的哈希值, 是同时由x和y来生成的. 体现在catlike coding给出的代码中:

LatticeSpan
	x = GetLatticeSpan(positions.c0), z = GetLatticeSpan(positions.c2);

Hash h0 = hash.Eat(x.p0), h1 = hash.Eat(x.p1);

(这里GetLatticeSpan的作用是获取当前坐标的向下取整和向上取整的整数值, 存储在p0和p1中, 并且将x - [x]存储在t中用于后续插值).

可以看到, 这里先是用x来生成了两个哈希值.

return lerp(
	lerp(h0.Eat(z.p0).Floats01A, h0.Eat(z.p1).Floats01A, z.t),
	lerp(h1.Eat(z.p0).Floats01A, h1.Eat(z.p1).Floats01A, z.t),
	x.t
)

在最后lerp的时候, 先用z再次改变hash之后, 才进行插值.

另一个问题就是代码中的z和x顺序是否可调换. 目前看下来调换应该没什么太大影响, 不过调换顺序可能导致生成的随机数改变, 也就是说调换顺序前后生成的结果不一样, 但由于都是随机的, 所以都能用吧.

值噪声在lerp的最后一个参数仍可改进, 使用smoothstep(一阶导保持连续性)或更优的(在二阶导也保持连续性)函数能够得到更加平滑连续的噪声结果. 关于这方面的优化可以见柏林噪声的改进部分.

柏林噪声 Perlin Noise

梯度函数

柏林噪声是梯度噪声(gradient noise)的一种. 所谓梯度噪声相比于前面的值噪声的区别就是: 值噪声是每个顶点有一个随机数生成的常数值, 而梯度噪声则是每个顶点有自己的函数. 显然, 最简单的函数形式就是一个常数值, 因此也可以将值噪声作为梯度噪声的简单情况.

这里的函数形式上就比较自由了, 以catlike coding中给出的代码为例, 它为一个函数传入的参数为: 当前网格点的随机数, 以及相对坐标(从网格点到当前顶点).

以一维情况举例. 假设x = 0.3, 其对应的网格点应该是0和1(分别向下和向上取整). 然后相对坐标就是从0到0.3, 即0.3. 我们还可以引入另一个相对坐标, 即从0.3到1, 不过不太符合我们的定义, 正确的应该是从1到0.3, 也就是-0.7.

从坐标的角度来说, 就是当前点的坐标减去网格点的坐标, 即为相对坐标.

有了这两个参数, 然后进行函数映射, 具体怎么映射就看需要了. 柏林噪声就是在这个基础上实现了一个函数. 而我们的值噪声则也可以视为这样一个函数, 它接收了随机数和相对坐标, 但只是返回了它接收到的随机数.

柏林噪声原理

先放一下视频给出的柏林噪声原理讲解:

柏林噪声的计算方法与值噪声类似,, 但区别在于其选取的点并非与值噪声一样是相邻的坐标值.

就二维的情况来说, 它和值噪声都是使用双线性插值来生成噪声.

这里直接讲柏林噪声是如何选取待混合值的.

对于一个二维的网格, 为所有顶点生成随机的梯度向量, 它们的x, y值范围都在-1到1之间.

给定一个位置及其所在晶格的四个顶点, 获取它们的梯度向量, 以及从四个顶点到给定点的距离向量, 将它们做点积.

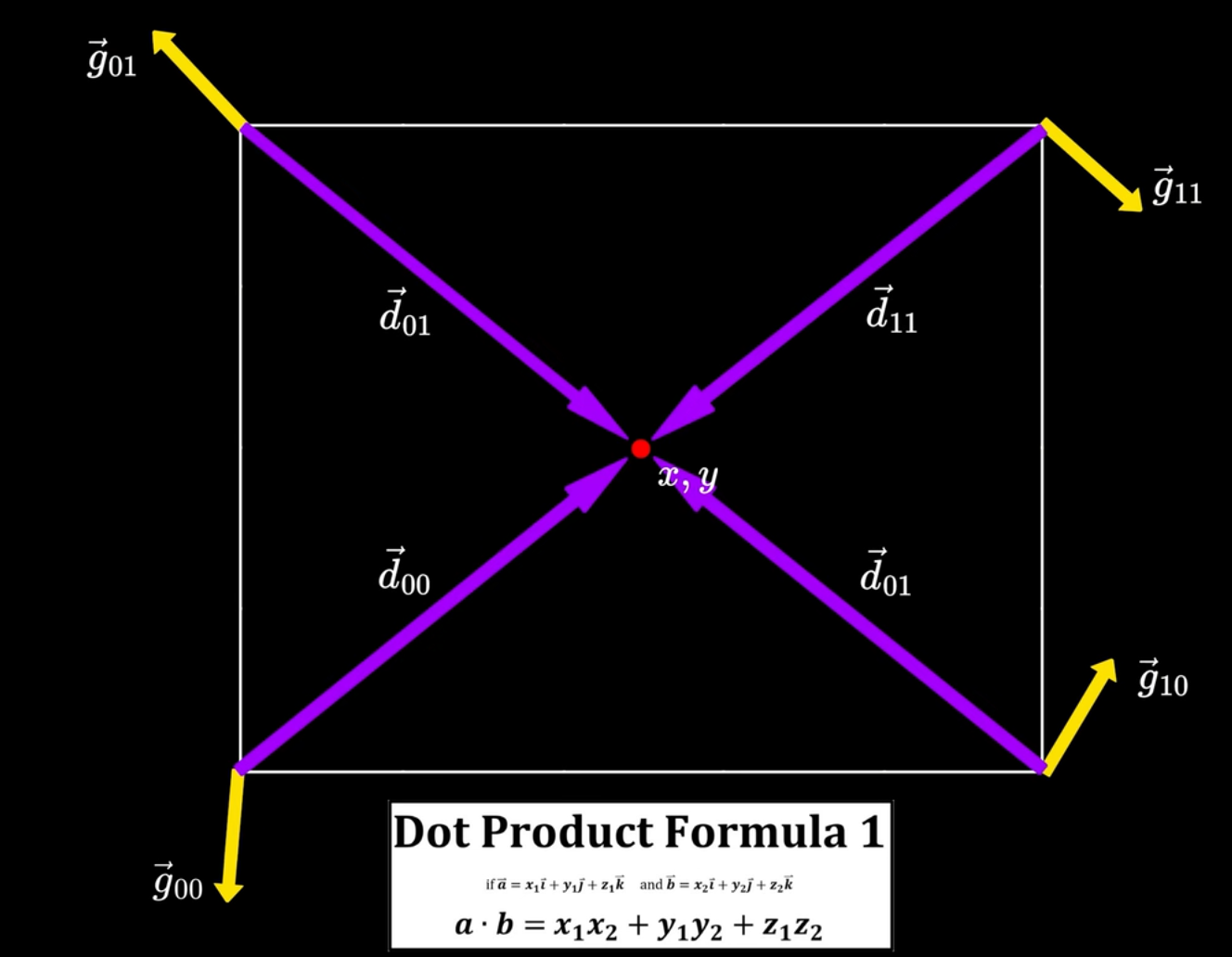
代入公式:

改进后的柏林噪声算法

上面讲的是初版柏林噪声算法.

在效果上, 由于可能会出现多个邻近顶点生成的梯度向量指向同一个方向, 会出现方向性伪影的情况.

改进方法, 一种是让梯度向量的生成分布更加均匀. 比如我们刚才生成的梯度向量是在一个正方形中(二维, xy值都在-1到1之间). 可以通过一些数学运算让梯度向量生成在一个圆中(三维情况下分别对应的就是正方体和球).

另一种则是使用预设定好的几个梯度向量, 然后随机选取. 这种方法的好处就是复现难度低, 更加可控的同时还能够大大降低运算量.

然后, 另一个缺陷是lerp的最后一个参数. 在这一块我们主要希望最终生成的噪声整体更加平滑连续, 而其中最重要的就是让每个网格的边界处衔接上. smoothstep在这方面会出现问题, 因为其二阶导数在边界处无法匹配(导致凹凸性改变).

我们需要一个在二阶导数中边界能够匹配的函数, 同时又具有smoothstep一样的平滑性. 最后得到的是:

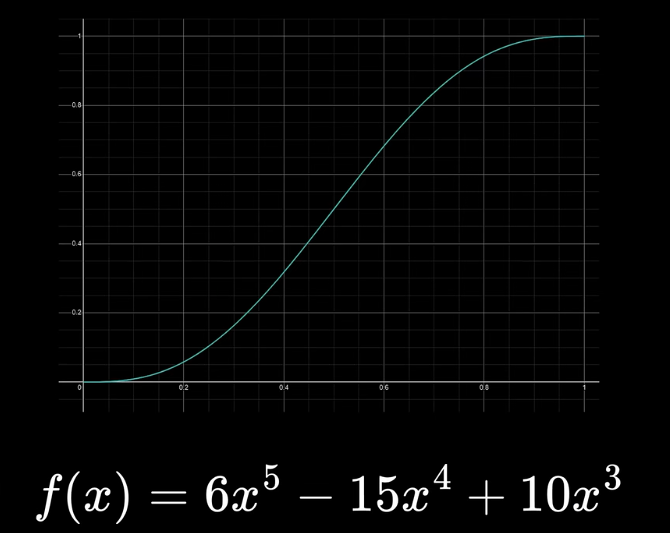
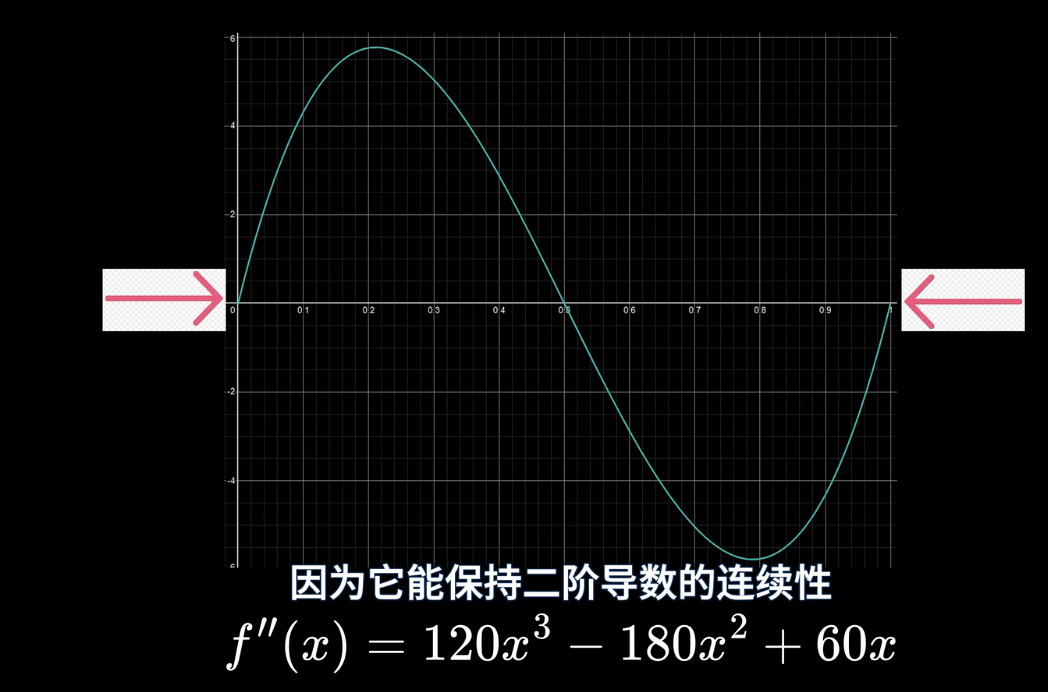
柏林噪声至此暂时结束了. 不过依旧没能完全解决方向性伪影的问题.

catlike coding的实现

仅看原理讲解有点泛, 具体来说, 每个点的梯度向量如何生成呢?

还记得一开始在梯度噪声部分提到的, 每个顶点有自己的函数吗? 在catlike coding中, 函数传入的参数是: 随机数, 以及相对坐标,

我们从二维的情况开始(因为我没看懂原文一维情况怎么算的). 简单来说, 我们通过随机数生成一个在正方形内部的二维坐标, 这个二维坐标就作为我们的二维梯度向量, 与相对坐标向量进行点积, 得到待混合的值.

(注: 下面这个hash自行转化为-1到1之间的浮点数)

public float Evaluate (Hash hash, float x, float y) {
	float gx = hash;
	float gy = 0.5f - abs(gx);
	gx -= floor(gx + 0.5f);
	return (gx * x + gy * y) * 2;
}

(最后乘二是为了让轴对齐向量的长度为1)

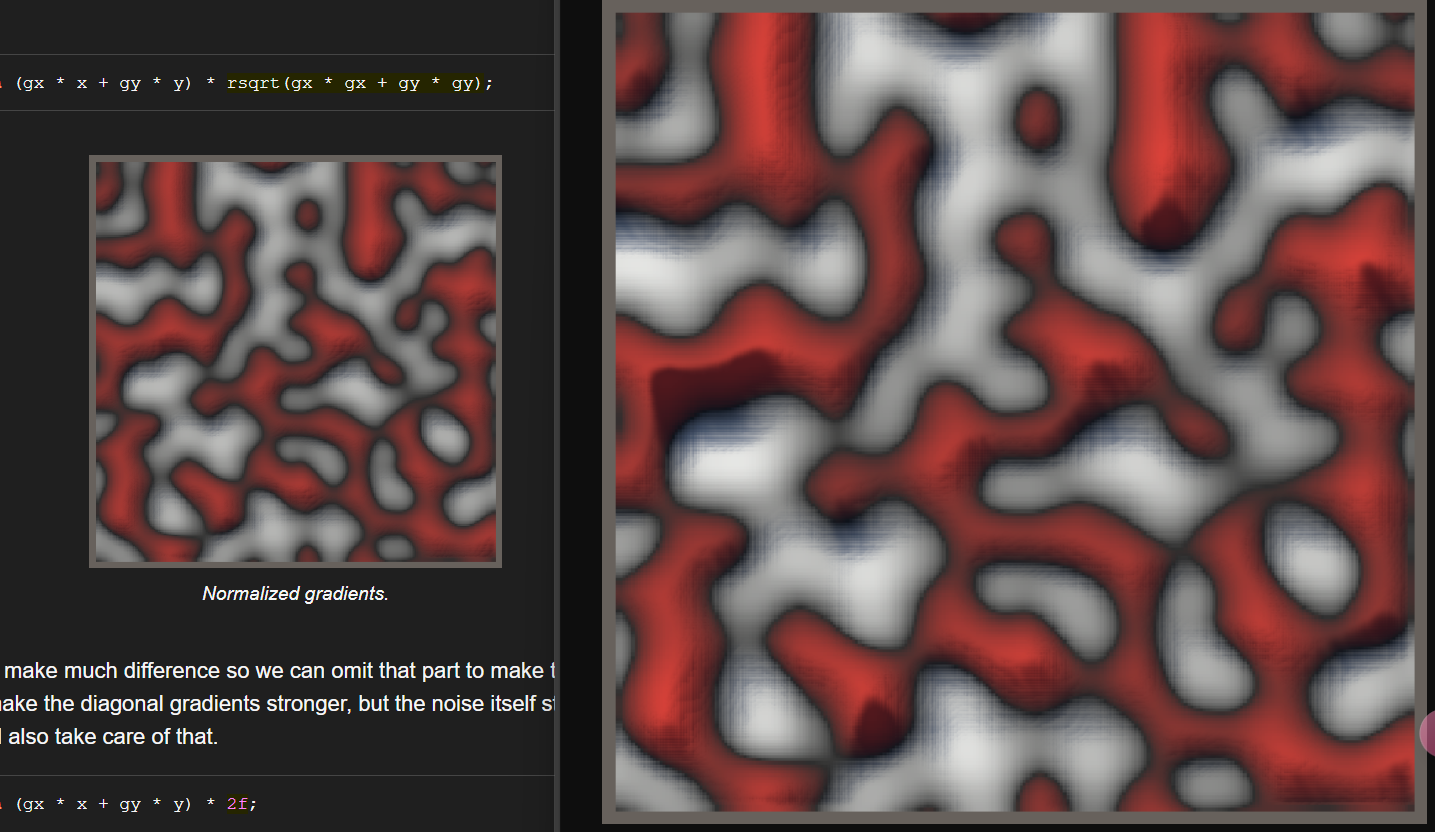
至于中间这个用随机数生成正方形内部的二维坐标的过程, 简单来说, 先得到纵坐标的取值, 然后将负的部分平移, 补成一个正方体. 这个过程可能比较抽象.

最后会涉及归一化问题, 也就是让结果在0-1之间

这部分内容确实没看懂, 最后作者结合缓动函数算出来是:

return (gx * x + gy * y) * (2f / 0.53528f);

我这边上个对比图, 我是没看出归一化前后有什么区别的...

三维的情况也类似, 这里不过多赘述. 给出代码实现:

(hash0和hash1是根据hash生成的-1到1的浮点数, 请自行生成)

public float Evaluate (Hash hash, float x, float y, float z) {
	float gx = hash0, gy = hash1;
	float gz = 1f - abs(gx) - abs(gy);
	float offset = max(-gz, 0f);
	gx += select(-offset, offset, gx < 0f);
	gy += select(-offset, offset, gy < 0f);
	return (gx * x + gy * y + gz * z) * (1f / 0.56290f);
}

噪声变体(分形, 湍流, 平铺)

分形 Fractal

不懂分形概念的读者可以先自行百度一下.

自然界中的分形也非常常见, 比如树枝的分叉, 植物的根等等. 在噪声生成的时候应用分形可以得到细节更加丰富, 整体更加自然的结果.

这里先给出分形实现的主要循环:

for (int o = 0; o < settings.octaves; o++){
    sum += amplitude * default(N).GetNoise4(position, hash + o, frequency);
    frequency *= settings.lacunarity;
    amplitude *= settings.persistence;
    amplitudeSum += amplitude;
}
noise[i] = sum / amplitudeSum;

octaves(八度)代表我们希望分形进行的次数. 完美的分形应当有无限个八度, 但显然我们不可能让计算机去做这件事. 一般来说, 分形6次已经效果足够好了.

amlitude代表振幅, 从抽象层面上理解, 我们是希望让每次分形得到的噪声对整体的影响越来越小. 振幅减小的速度我们使用persistence来调整.

frequency代表当前分形计算噪声的时候所用的频率. 正常来说, 我们会让frequency在每次迭代都加倍. 在此使用lacunarity来控制. frequency的缩放称为噪声的空缺性. 当lacunarity越大, 意味着每一个八度之间的空隙越多.

每次循环, 将结果加上当前分形计算得到的噪声. 在退出循环后, 会将sum归一化, 防止得到超出-1到1范围的噪声.

另外在计算噪声的时候, 我们会将hash加上当前迭代次数. 本质上是希望用连续的种子生成随机数, 从而减少每次分形的重复性.

关于getnoise函数的计算, 可见项目代码或原教程.

湍流 Turbulence

关于湍流的概念, 我一开始没太看懂原文的解释, 所以问了ai:

大概...懂了一点...?

还记得我们生成噪声的时候, 最后一步是lerp插值吗? 现在我们要在插值之后再做一些计算.

其实很简单, 在生成噪声时, 只要把结果取个绝对值即可. 这里不放代码了.

看看效果图.

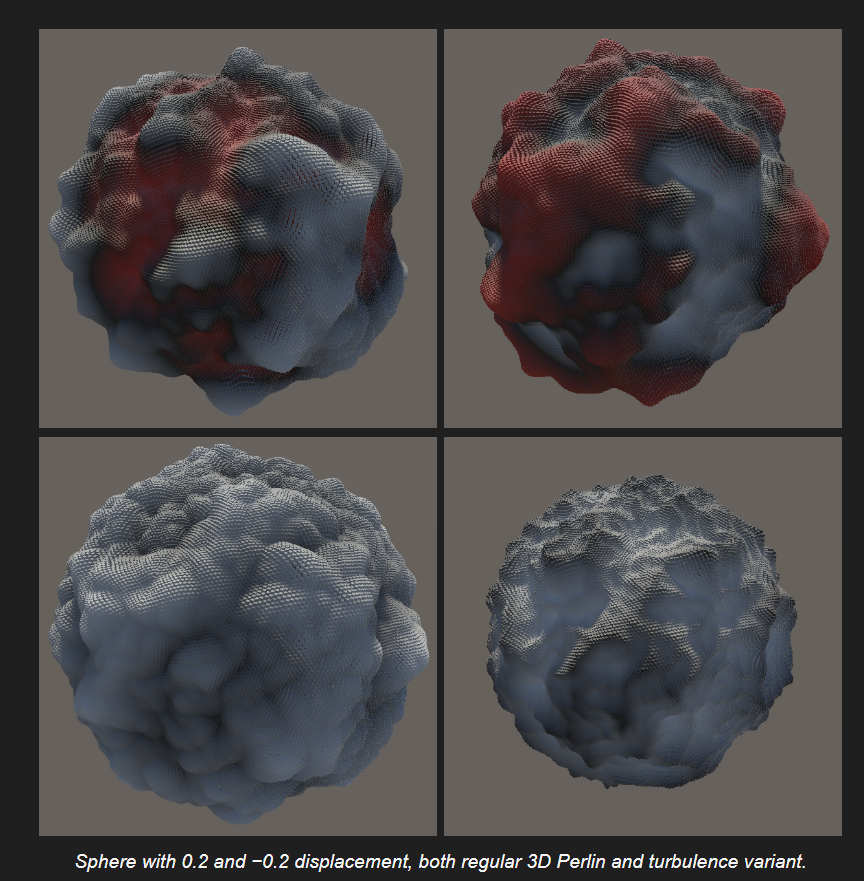
平铺噪声 Tiling Noise

这种噪声, 会用于重复纹理的生成, 比如我们家里地砖的图案. 每个地砖都使用相同的纹理, 但是拼接起来却能够连上.

平铺噪声操作的地方主要是在网格顶点上. 回忆一下我们前面提到的噪声计算, 我们通过当前顶点向下取整和向上取整得到网格顶点. 现在依旧这么做, 并且正常生成相对坐标. 不过, 在生成相对坐标之后, 我们会再将网格顶点取余频率, 从而实现"周期性", 这是平铺噪声的第一个计算细节. 这里的频率就是我们前面分形中的frequency.

span.p0 %= frequency;
span.p1 %= frequency;

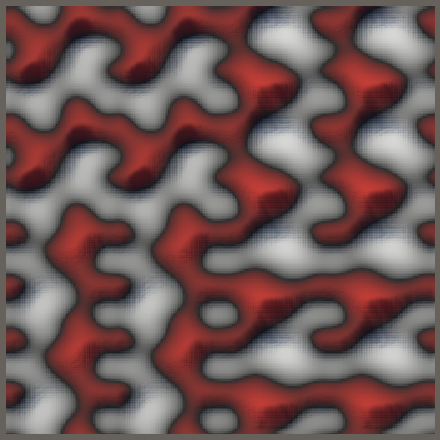
One octave frequency 2 tiling 2D Perlin; domain scale 4.

可以看到并不正确, 四个角落分别对应四个不同的图案. 这是因为余数受到符号的影响. 这是平铺噪声的第二个计算细节: 统一符号.

我们这样修复:

span.p0 %= frequency;
span.p0 = select(span.p0, span.p0 + frequency, span.p0 < 0);
span.p1 = (span.p0 + 1) % frequency;

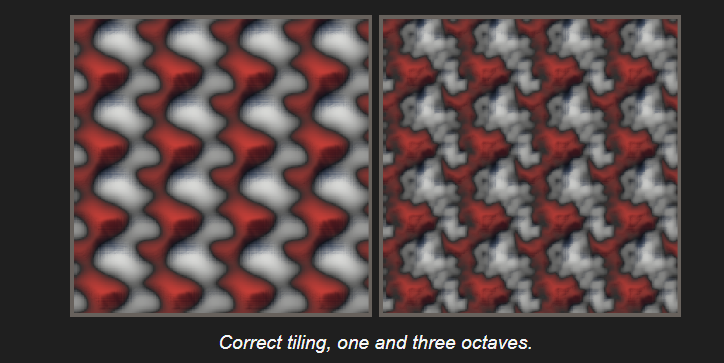
来看看平铺的效果.

这里顺便贴一下原文避开取余操作的计算方法:

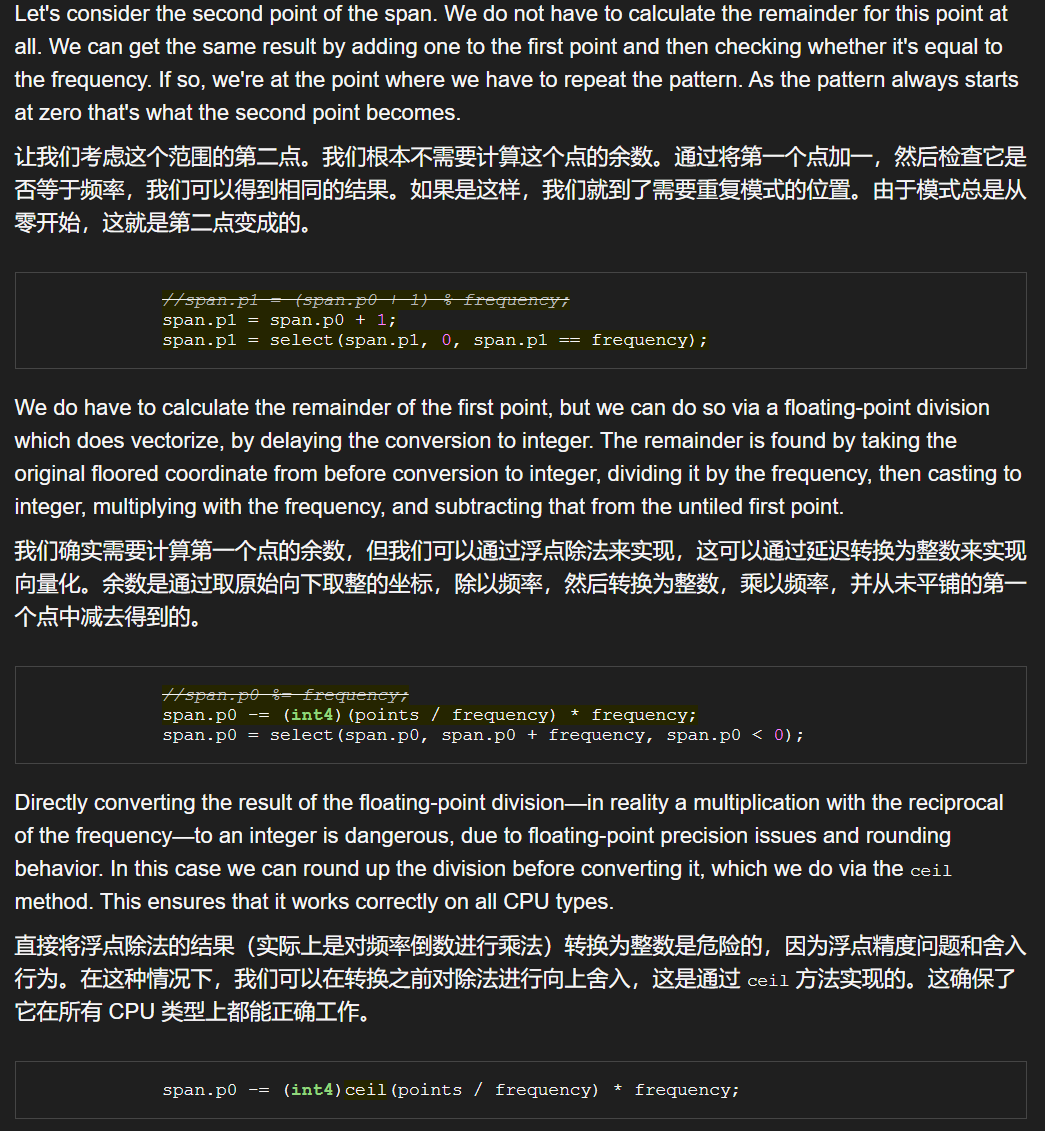
可以回忆一下, 求余数的过程, 把过程逆过来推一下即可. 比如3除以2等于1余1, 那么就有3 = 2 * 1 + 1, 那么余数1 = 3 - 2 * 1. 上面给出的代码中, point是当前点向下取整. 可以视为这里的span.p0, 也即式中的3, 然后 points / frequency就是1, frequency就是2.

沃洛诺伊噪声 Voronoi Noise

模拟自然界中一块一块的网格形状. (比如蛇的表皮) 以二维情况举例, 先在二维空间中生成一系列随机的点, 然后在着色的时候根据距离当前像素最近的点进行着色.

这种类型的噪声最初由Steven Worley引入，因此也被称为Worley Noise。

还记得我们前面讲梯度噪声的时候提到的, 每个顶点都有自己的函数吗? Voronoi噪声也是这样, 只不过柏林噪声每个顶点的函数是生成梯度向量并点乘相对坐标向量, 而Voronoi噪声每个顶点的函数是计算离当前顶点最近的(前面提到的, 随机生成的)点的距离.

并且, 这个函数的传入参数依旧是随机数和相对坐标.

函数内部的实现思路是: 我们会用向下取整得到的顶点所对应的hash值, 来在当前网格生成一个随机顶点. 同样的, 在相邻的网格生成随机顶点, 最后在这几个随机顶点和当前顶点之间计算最小距离.

来看一维的情况:

代码逻辑基本遵顼上面讲的思路.

得益于伪随机的固定生成逻辑, 我们可以轻易地多次获取相邻顶点的hash值. 在迭代中更新最小值, 这个是比较常规的if判断更新. 后面的abs(...)就是距离.

代码中的g0代表当前坐标相对于向下取整顶点的距离. 可以认为是相对坐标. 另外一个比较重要的点是, 我们使用hash.float为随机数生成一个浮点数, 这个浮点数已经保证了在0到1的范围之内, 无需担心其"在世界任意位置生成坐标而非在网格内生成".

float minima = 2f;
for (int u = -1; u <= 1; u++) {
	Hash h = hash.Eat(x.p0 + u);
	minima = UpdateVoronoiMinima(minima, abs(h.Float + u - x.g0));
}
return minima;

对平铺噪声情况优化

如果希望使用平铺噪声, 那么在迭代的时候, 相邻网格可能会辐射到重复采样区域之外的地方.

那么优化的逻辑就是: 如果右侧相邻网格超出了重复采样区域, 就回到0, 如果左侧超出区域, 就回到最右侧.
public int ValidateSingleStep (int points, int frequency) =>
	select(select(points, 0, points == frequency), frequency - 1, points == -1);
把这个优化放在hash生成那一步.
float minima = 2f;
for (int u = -1; u <= 1; u++) {
	Hash h = hash.Eat(ValidateSingleStep(x.p0 + u, frequency));
	minima = UpdateVoronoiMinima(minima, abs(h.Float + u - x.g0));
}
return minima;

再来看二维的情况. 显然, 求距离就需要使用勾股定理了.

float GetDistance (float x, float y) => sqrt(x * x + y * y);

思路是这样的: 用同样的方法生成顶点. 这次是二维的, 所以分别用x和z来生成一个hash. 两次for循环. 第一次计算x方向上的偏移量, 第二次计算z方向上的偏移量, 最后勾股定理计算距离. 基本上只是从一维拓展到二维, 没有太多难点. 生成二维随机顶点的时候用了h.float1和h.float2. 这里的offset如果看不懂什么意思, 可以回看一下一维的情况. 说是个offset, 倒是更像个单纯的把计算公式中的后半部分提生成一个变量而已.

float4 minima = 2f;
for (int u = -1; u <= 1; u++) {
	Hash hx = hash.Eat(l.ValidateSingleStep(x.p0 + u, frequency));
	float xOffset = u - x.g0;
	for (int v = -1; v <= 1; v++) {
		Hash h = hx.Eat(l.ValidateSingleStep(z.p0 + v, frequency));
		float zOffset = v - z.g0;
		minima = UpdateVoronoiMinima(minima, GetDistance(
			h.Float1 + xOffset, h.Float2 + zOffset
		));
	}
}
return minima;

结果符合我们的预期, 黑点就是每个网格生成的随机坐标, 颜色深浅代表当前像素与随机点的最近距离.

还有一个问题就是, 我们最后得到的最小距离有可能大于一. 想象一个网格, 如果随机生成点在右下角, 而我们当前像素在左上角, 那么距离就是根号二了, 而该像素此时与相邻网格中的随机生成的点之间的距离也可能会是大于1的. 在这样的情况下, 有可能离当前像素最近的随机生成点并不在相邻的网格内, 而是在更远的网格内. 我们不会考虑这种情况, 因为这样会让计算效率降低, 也会让计算变得更复杂, 噪声结果变得难以预测.

事实上, 距离超过1的情况不算少见. 我们希望讲值限制在0到1之间, 所以对于超过1的值, 我们会让其取1. 但这样就会出现很多距离都为1的区域, 表现为大块的白色, 如上图所见, 边缘处会有很多白色的间隙.

对此, 我们希望减少距离超过1的情况. 优化方法是: 同一个网格中生成两个随机点.

float4 minima = 2f;
for (int u = -1; u <= 1; u++) {
	Hash hx = hash.Eat(ValidateSingleStep(x.p0 + u, frequency));
	float xOffset = u - x.g0;
	for (int v = -1; v <= 1; v++) {
		Hash h = hx.Eat(ValidateSingleStep(z.p0 + v, frequency));
		float zOffset = v - z.g0;
		minima = UpdateVoronoiMinima(minima, GetDistance(
			h.Float1 + xOffset, h.Float2 + zOffset
		));
		minima = UpdateVoronoiMinima(minima, GetDistance(
			h.Float3 + xOffset, h.Float3 + zOffset
		));
	}
}
return minima;

我截了个对比图, 可以看看效果. 很明显右边块与块之间是要更紧凑的.

三维的情况同理可以拓展得到. 这里不多赘述. 可视化效果下, 非常像多肉hhh

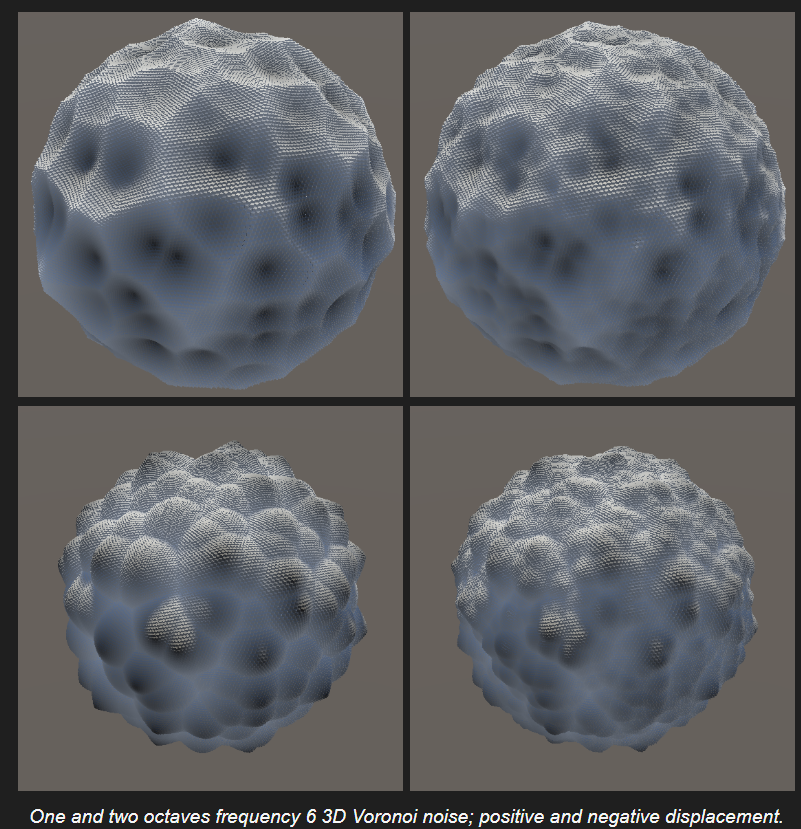
第二距离

我们不仅可以计算最近距离的点, 还可以计算第二近距离, 第三近距离, 或者第二近距离减去第一近距离等等.

第三近距离的情况下, 大部分噪声值都大于一, 所以我们选择第二近的. 计算方法也很简单, 用两个变量分别存储第一近和第二近. 当第一近的更新, 那么第二近就是第一近的旧值. 可以想象, 总体会变得更"白", 因为更多噪声最终取了1.

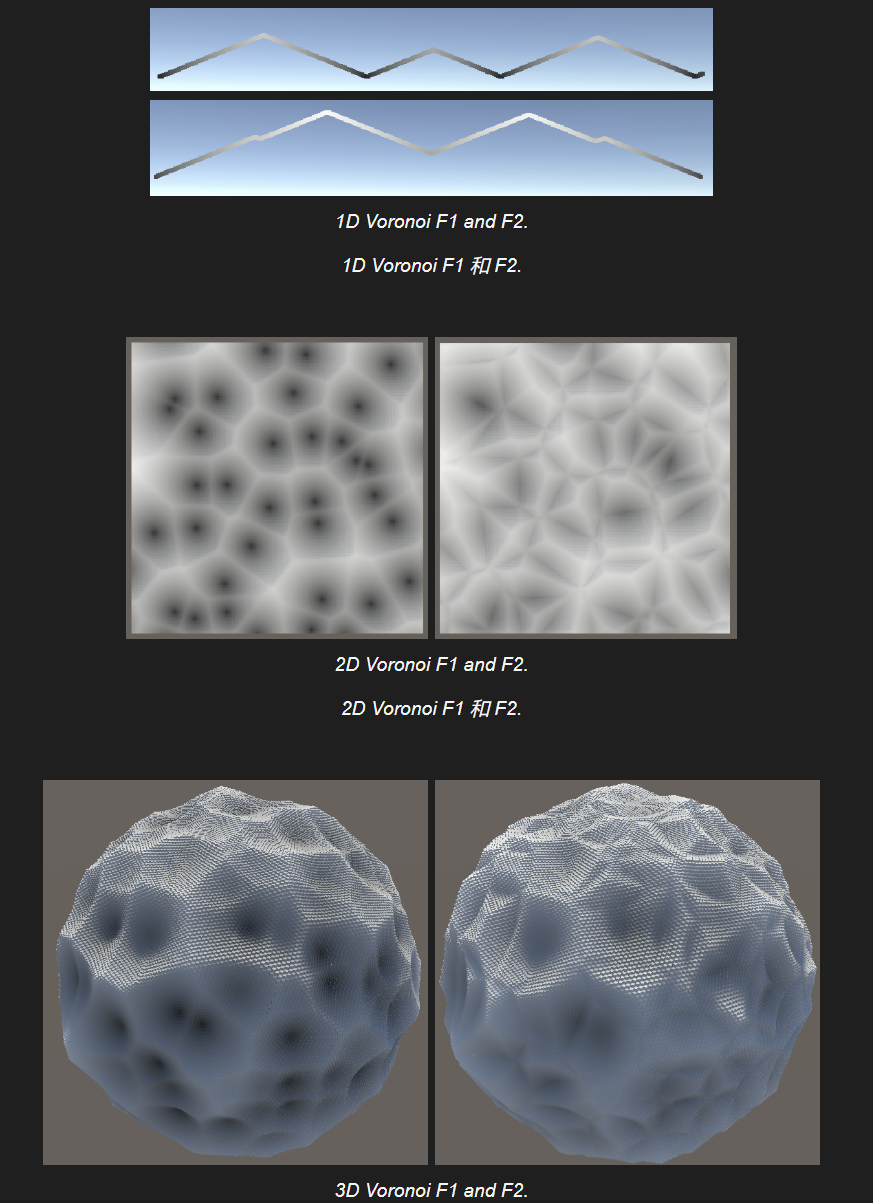
如果用第二近减去第一近的变体, 效果如下:

改变距离的计算方式

切比雪夫距离 / 棋盘距离

简单来说就是将计算距离的方式从勾股定理变成了"取最大值".

public float4 GetDistance (float4 x) => abs(x);

public float4 GetDistance (float4 x, float4 y) => max(abs(x), abs(y));

public float4 GetDistance (float4 x, float4 y, float4 z) =>
	max(max(abs(x), abs(y)), abs(z));

效果如下

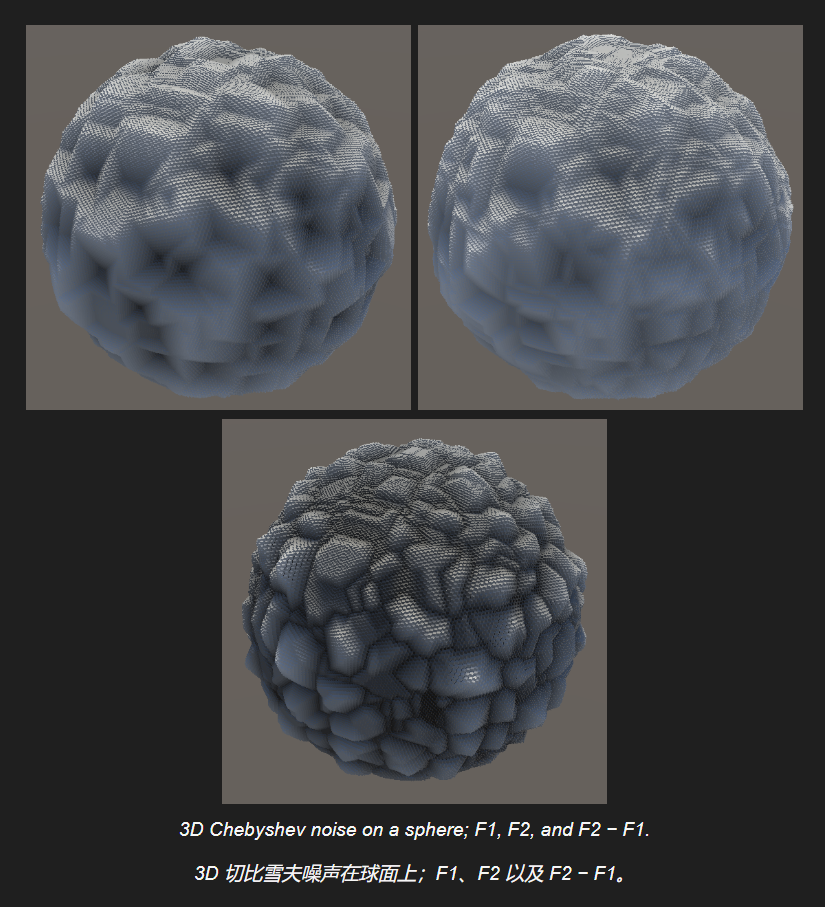
看起来会更加人工.

平方欧几里得距离

省略开根号的操作. 计算成本更低, 但总体效果没那么强烈. 原因是小于1的值在开根号后会变大, 如果不开根号, 那么算出来的距离就要更小.

曼哈顿距离

这种计算方式会让结果更大. 最后结果有点像切比雪夫距离的结果, 但是更白.

单形噪声 Simplex Noise

什么是单形?

单形是多面体中最简单的一种——具有平坦边界的对象，它占据所有可用维度中的空间。一条直线段是 1D 单形。一个三角形是 2D 单形。一个正方形不是 2D 单形，因为它比三角形多一个角和一边，因此不是最简单的形状。一条直线段也不是 2D 单形，因为它只有一个维度，无论它在 2D 空间中如何定向。最后，一个四面体是 3D 单形。

单形噪声不像柏林噪声和值噪声那样最后使用插值生成结果.. 单形噪声采用的是核函数的形式, 简单来说, 对各个网格点应用核函数, 最后求和后返回.

我们先从一维的单形噪声开始. 这里我概述一下原文的思路吧: (注意这里虽然是一维的情况, 但高维的情况也是基于该原理)首先将当前顶点向下取整, 得到网格点, 然后我们会用这个网格点生成hash值, 让核函数来处理这个点. 核函数中, 会计算出相对坐标, 然后对这个相对坐标应用径向对称衰减函数, 得到一个值, 记为f. 同时会使用hash和相对坐标生成梯度向量与相对坐标的点积结果, 最后用f乘以点积结果, 作为返回值返回. 同样地, 让网格点＋1(也就是当前点向上取整)能够得到另一个网格点, 让核函数处理它. 最后将两个核函数的计算结果相加后返回即可.

文字可能有点长, 但应该好理解. 中间出现了"径向衰减函数", 这个马上会讲. 作为结果, 先大概看一下函数.(再次强调, 是一维的情况)

public float GetNoise4 (float3 positions, Hash hash, int frequency) {
	positions *= frequency;
	int x0 = (int)floor(positions.x), x1 = x0 + 1;

	return Kernel(hash.Eat(x0), x0, positions) + Kernel(hash.Eat(x1), x1, positions);
}

这里用frequency对坐标进行了缩放, 是考虑了分形噪声的情况.

在看核函数之前, 可以先讨论一下径向对称衰减函数. 在simplex noise中, 它扮演了插值函数的角色. 这么说可能不太严谨, 换个说法就是: 它实现了与插值函数类似的效果.

这个函数在网格点处取1, 在达到相邻网格点的时候降至0. 两个方向都是如此. 我个人感觉这个函数有种"权重从当前网格点向两边衰减"的味道.

最简单的衰减函数就是: \(f(x) = 1 - |x|\). 显然它是符合我们刚才的描述的. 如果使用了这个函数, 那么核函数应该如下:

static float Kernel (Hash hash, float lx, float3 positions) {
	float x = positions.x - lx;
	float f = 1f - abs(x);
	return f * default(G).Evaluate(hash, x);
}

这里的default(G).Evaluate(hash, x)是用于生成梯度向量的函数. 这样会得到类似线性插值的效果.

1D Value simplex noise, linear falloff.

那么类比插值的情况, 我们想让他更平滑, 就需要在一阶导处连续, 同时在二阶导处连续. 这可以通过增加次方解决. 首先让\(f(x) = 1 - x ^ 2\).

Squared falloff. 平方衰减。

这样得到的结果变得稍微平滑了, 但它一阶导和二阶导都不是连续的.(在x取1和-1的时候值不为零). 而且还会有噪声值超过1的情况. 比如当x = 0.5, 那么结果是0.75, 两个核函数相加就是1.5.

增加\(f(x)\)的次方, 我们能够得到答案: \(f(x) = (1 - x^2)^2\). 它的导数是: \(f'(x) = 4x^3 - 4x\), 一阶导连续. 不过其二阶导依旧不连续. 将平方改成立方, 就得到最终答案了.

\[ f(x) = (1 - x^2)^3 \]

最后的核函数:

static float Kernel (Hash hash, float lx, float3 positions) {
	float x = positions.x - lx;
	float f = 1f - abs(x);
	f = f * f * f;
	return f * default(G).Evaluate(hash, x);
}

与常规值噪声的一维情况对比一下.

在二维的情况下, \(x^2\) 改为 \(d\), 代表平方距离, 即勾股定理但不开根号.

static float Kernel (
	Hash hash, float lx, float lz, float3 positions
) {
	float x = positions.x - lx, z = positions.z - lz;
	float4 f = 1f - x * x - z * z;
	f = f * f * f;
	return f * default(G).Evaluate(hash, x, z);
}

其生成噪声的函数如下

public float GetNoise4 (float3 positions, Hash hash, int frequency) {
	positions *= frequency;
	int
		x0 = (int)floor(positions.x), x1 = x0 + 1,
		z0 = (int)floor(positions.z), z1 = z0 + 1;

	Hash h0 = hash.Eat(x0), h1 = hash.Eat(x1);

	return (
		Kernel(h0.Eat(z0), x0, z0, positions) +
		Kernel(h0.Eat(z1), x0, z1, positions) +
		Kernel(h1.Eat(z0), x1, z0, positions) +
		Kernel(h1.Eat(z1), x1, z1, positions)
	);
}

Radial falloff with square lattice; frequency 4.

这个图大体上符合结果. 不过在边缘处有明显的黑色, 这是因为距离超过1的时候核函数的计算结果是负值. 我们稍微修改即可.return max(0f, f) * default(G).Evaluate(hash, x, z);

Clamped kernels

不过我们现在使用的是正方形网格, 并非单形. 我们希望将网格从正方形变为等边三角形. 因为它是二维空间下的单形. 现在先考虑从正方形转变为菱形.

原文推导过程: 简单噪声 --- Simplex Noise 这里不翻译了, 直接贴结论. 就是x和z同时减去\(((3-\sqrt3)/6) * (x+z)\), 这样可以直接将正方形压缩为菱形.

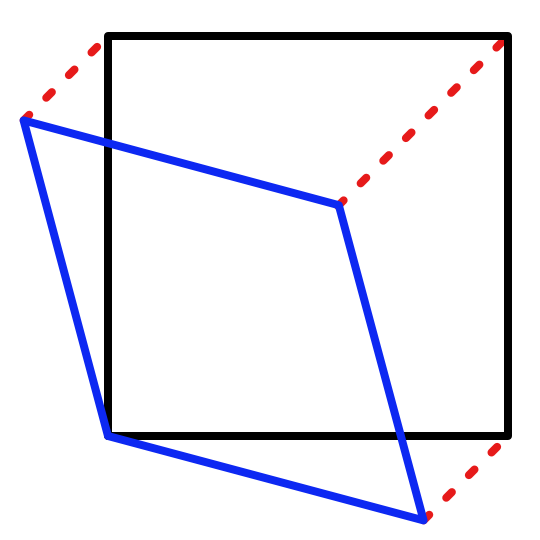
Skewing from square to rhombus.

我们还需要推导从三角形网格变为正方形网格的结论. 显然应该是x和z同时加上一个数. 这里同样直接给出结论: \(((\sqrt3 - 1)/2) * (x+z)\). 当然由于三角形并非四个点, 我们这里所谓"转化为正方形"是指将等边三角形的三个点都放在正方形对应的位置上, 变成等腰直角三角形. 坐标分别是(0, 0), (0, 1)或(1, 0), 以及(1, 1).

看到这里你可能依旧在疑惑, 算这俩干嘛? 我一开始也没太懂, 后面琢磨半天才绕过来. 这样, 您先想象一下一个二维空间, 由无数等边三角形构成.(是的, 我们现在以单形作为基本采样网格, 而非正方形). 现在我们想通过当前点获取网格的顶点, 但不好获取. 所以我们第一步是将当前顶点映射到由正方形网格构成的二维空间. 然后向我们之前一样, 向上取整, 向下取整, 就得到了网格点了, 之后再映射回来, 不就是我们三角形网格的顶点吗?

所以第一步, 就是获得正方形网格构成的二维空间下的网格点.

positions *= frequency;
float skew = (positions.c + positions.z) * ((sqrt(3f) - 1f) / 2f);
float sx = positions.x + skew, sz = positions.z + skew;
int
	x0 = (int)floor(sx), x1 = x0 + 1,
	z0 = (int)floor(sz), z1 = z0 + 1;

第二步, 调整核函数. 因为我们获取了正方形网格构成的二维空间下的网格点, 传给核函数去计算, 那么核函数计算的时候, 需要将这个网格点映射回三角形网格构成的二维空间.

float unskew = (lx + lz) * ((3f - sqrt(3f)) / 6f);
float x = positions.x - lx + unskew, z = positions.z - lz + unskew;
float f = 1f - x * x - z * z;

这样得到的结果会是过曝的白色, 这是因为三角形比正方形要小, 它的衰减应该更快才行. 将1改成0.5.

float f = 0.5f - x * x - z * z;

这个0.5也是有讲究的. 我们希望从等边三角形左下角顶点到右边中点处时衰减到0. 这个数值即为等边三角形的高. 结合原文推到过程最后得到的高的平方恰为0.5.

Un-skewed kernels, but weak.

现在又太弱了, 这是因为左下角的顶点处本身的衰减系数就很低, \(f(0, 0) = 1/8\), 我们乘个8即可.

f = f * f * f * 8f;

Maximum amplitude; still frequency 4

剩下的一个小问题是, 三角形的频率要比正方形更高. 我们可以缩放一下频率.

positions *= frequency * (1f / sqrt(3f));

这个缩放因子也有讲究.

核函数返回值:

return max(0f, f) * default(G).Evaluate(hash, x, z);

相比于常规的值噪声, 单形噪声更弱, 同时形似蜂窝状.

另外, 我们目前依旧是采用四个核函数相加后返回. 而实际上每个三角形只需要三个内核. 我们可以通过判断x和z的大小关系决定使用右下角的顶点还是左上角的顶点. 当x>z的时候, 就选择右下角, 否则选择左上角. 最后返回.

return (
	Kernel(h0.Eat(z0), x0, z0, positions) +
	Kernel(h1.Eat(z1), x1, z1, positions) +
	Kernel(hC.Eat(zC), xC, zC, positions)
);

二维的单形噪声到这里的就结束了.

三维的情况也需要好好讲一下. 相比二维, 三维是将正方体网格给压缩为菱柱

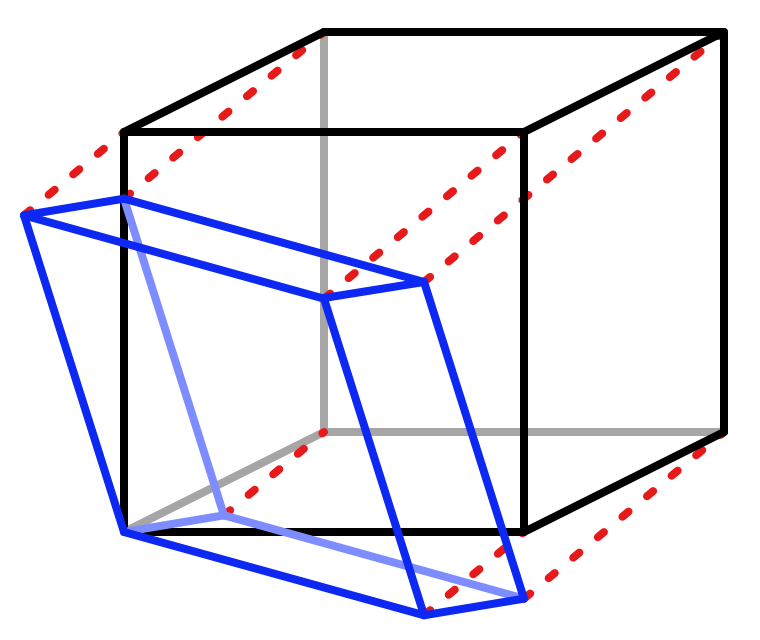
Skewing from cube to rhombohedron.

其从菱柱到正方体的因子为1/3, 从正方体到菱柱的因子为1/6.

由于我们三维空间下的单形是四面体, 我们考虑的是: 从左下角顶点出发到右上角(即体对角线上的两个顶点), 将正方体分成六个四面体. 我们采样的空间是由无数个正四面体构成, 而非正方体. 由正四面体转为正方体, 由于四面体只有四个点, 那么实际上是由正四面体转为直角四面体. 然后, 对频率的因子缩放是0.6, 而衰减函数的第一个常数依旧是0.5.

一个重点是判断选择哪个四面体.

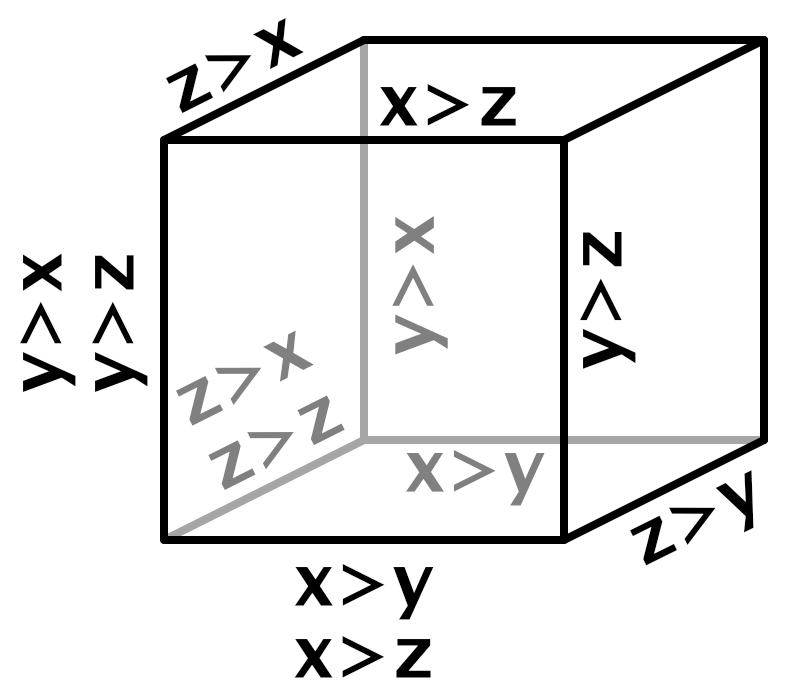
Choosing kernels in two steps; the greater-than signs match walk direction.

在二维情况下, 我们通过比较xz的大小来判断选择哪个点, 在三维情况下, 需要同时比较xyz的大小, 来判断需要选哪两个点. 实现思路也很简单, 列出真值表, 然后根据真值选择最后的点.

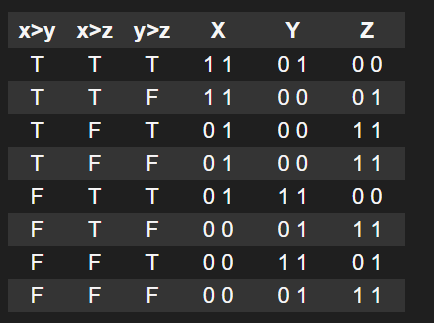
bool
	xGy = sx - x0 > sy - y0,
	xGz = sx - x0 > sz - z0,
	yGz = sy - y0 > sz - z0;

bool
	xA = xGy & xGz,
	xB = xGy | (xGz & yGz),
	yA = !xGy & yGz,
	yB = !xGy | (xGz & yGz),
	zA = (xGy & !xGz) | (!xGy & !yGz),
	zB = !(xGz & yGz);
int
	xCA = select(x0, x1, xA),
	xCB = select(x0, x1, xB),
	yCA = select(y0, y1, yA),
	yCB = select(y0, y1, yB),
	zCA = select(z0, z1, zA),
	zCB = select(z0, z1, zB);

最后


return (
	Kernel(h0.Eat(y0).Eat(z0), x0, y0, z0, positions) +
	Kernel(h1.Eat(y1).Eat(z1), x1, y1, z1, positions) +
	Kernel(hA.Eat(yCA).Eat(zCA), xCA, yCA, zCA, positions) +
	Kernel(hB.Eat(yCB).Eat(zCB), xCB, yCB, zCB, positions)
);

至此, 三个维度的单形噪声, 我们实现了大半了.

剩下的那一部分主要是处理梯度向量的生成. 我们前面是直接套用的柏林噪声中的梯度向量生成函数(也就是接收随机数与相对坐标, 生成梯度向量并与相对坐标进行点积后返回的那个函数). 但这个函数是适配正方形和正方体网格的. 为了给我们的单形噪声弄一个适配的梯度向量生成函数, 我们将基于圆和球面来生成梯度向量.

原理依旧是生成分布在正方形和正方体中的随机坐标, 只不过我们会将它们归一化.

这里我不考虑一维的情况.

还记得我们柏林噪声中生成梯度向量得函数吗?

static float2 SquareVectors (Hash hash) {
	float2 v;
	v.x = hash.Float * 2f - 1f;
	v.y = 0.5f - abs(v.c0);
	v.x -= floor(v.x + 0.5f);
	return v;
}

在点积的时候, 正常是这样:

public static float Square (Hash hash, float x, float y) {
	float2 v = SquareVectors(hash);
	return v.x * x + v.y * y;
}

圆形的话是这样:

public static float Circle (Hash hash, float x, float y) {
	float2 v = SquareVectors(hash);
	return (v.x * x + v.y * y) * rsqrt(v.x * v.x + v.y * v.y);
}

最后归一化. 这个缩放因子的推导同样可见原教程.

return (v.x * x + v.y * y) * rsqrt(v.x * v.x + v.y * v.y) * (5.832f / sqrt(2f));

这是二维的情况, 三维的情况也类似, 将八面体的梯度向量生成改成球体的梯度向量生成.

static float3 OctahedronVectors (SmallXXHash hash) {
	float3 g;
	g.x = hash.Float * 2f - 1f;
	g.y = hash.Float * 2f - 1f;
	g.z = 1f - abs(g.x) - abs(g.y);
	float offset = max(-g.z, 0f);
	g.x += select(-offset, offset, g.x < 0f);
	g.y += select(-offset, offset, g.y < 0f);
	return g;
}		

public static float Sphere (Hash hash, float x, float y, float z) {
	float3 v = OctahedronVectors(hash);
	return
		(v.x * x + v.y * y + v.z * z) *
		rsqrt(v.x * v.x + v.y * v.y + v.z * v.z);
}

缩放

return
	(v.x * x + v.y * y + v.z * z) *
	rsqrt(v.x * v.x + v.y * v.y + v.z * v.z) * (1024f / (125f * sqrt(3f)));

到此结束了. 哎, 终于, 这也太多了...

‍

后记

这篇文章本来是笔记的. 我发现一边看教程一边敲代码一边理解一边记笔记, 有点费劲了, 经常就是理解没能跟上, 光在敲代码和记笔记. 就换了个策略, 优先过一遍教程, 确保每一步都能够理解, 然后写成笔记, 最后再跟着敲一遍. 实测下来效果非常好, 而且速度并不慢, 同时能够获得一种掌控感,. 个人认为这种学习策略对于教程类资料的学习效果是很不错的.

‍

随机数与噪声入门